Question

Would lines Y=-1/10x+6 and 10y+x=-100be perpendicular parallel or neither? I just need a brief explanation with the answer

Answer 1

Given:

The given equations are,

`\begin{gathered} y=-(1)/(10)x+6\text{ . .. . . . . (1)} \\ 10y+x=100\text{ . . . . . .(2)} \end{gathered}`

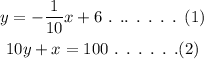
The objective is to find whether these two lines are parallel, perpendicular or neither.

Step-by-step explanation:

The general eqauation of straight line is,

`y=mx+b_{}`

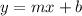
Here, m represents the slope of the straight line, b represents the y intercept.

For parallel lines, the slope value of both the lines will be equal.

`m_1=m_2`

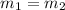
For perpendicular lines, the slope value both the lines will be opposite and inverse.

`m_1=-(1)/(m_2)`

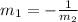
To find slope of line 1 and line 2:

By comparing the general equation with the equation (1), the slope value of equation (1) will be,

`m_1=-(1)/(10)`

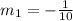
The equation (2) can be solved as,

`\begin{gathered} 10y+x=100 \\ 10y=-x+100 \\ y=-(1)/(10)x+(100)/(10) \\ y=-(1)/(10)x+10 \end{gathered}`

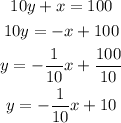
Now, by comparing the above equation with the general equation, the slope value of line 2 will be,

`m_2=-(1)/(10)`

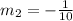
Thus, the slope value of line 1 and line 2 are equal which is -(1/10).

Hence, these two lines are parallel lines.