Question

Bill wanted to try out different water craft. He went 42 miles downstream in a motor boat and 76 miles downstream on a jet ski. His speed on the jet ski was 20 mph faster than in the motor boat. Bill spent a total of 4 hours on the water. What was his rate of speed, in miles per hour, in the motor boat

Answer 1

Answer:

The rate of speed of the motor boat is 20 mph

Step-by-step explanation:

The distance of the motor boat = 42 miles

The distance of the jet ski = 76 miles

let the speed of the motor boat = s

the speed of the jet ski = 20mph faster than the motor boat

the speed of the jet ski = 20 + s

Total time spent = 4 hours

To get the speed of the motor boat, we will apply the formula:

`\begin{gathered} speed\text{ = }(distance)/(time) \\ time\text{ = }(distance)/(speed) \end{gathered}`

Time for motor boat:

time = 42/s

Time for the jet ski:

time = 76/(20 + s)

Total time = time for the motor boat + time for the jet ski

`\begin{gathered} Total\text{ }time\text{ = }(42)/(s)\text{ + }\frac{76}{20\text{ + s}} \\ 4=(42)/(s)\text{ + }\frac{76}{20\text{ + s}} \\ \\ 4\text{ = }\frac{42(20\text{ + s\rparen + 76\lparen s\rparen}}{s(20\text{ + s\rparen}} \\ 4\text{ = }\frac{840\text{ + 42s + 76s}}{20s\text{ + s}^2} \\ 4(20s\text{ + s}^2)\text{ = 840 + 42s + 76s} \\ 80s\text{ + 4s}^2\text{ = 840 + 118s} \end{gathered}`
`\begin{gathered} 4s^2\text{ + 80s - 118s - 840 = 0} \\ 4s^2\text{ - 38s - 840 = 0} \\ \\ divide\text{ both sides by 2:} \\ 2s^2\text{ - 19s - 420 = 0} \end{gathered}`
`\begin{gathered} factorize\text{ 2s}^2\text{ - 19s - 420 = 0} \\ 2s^2\text{ - 40s + 21s - 420 = 0} \\ 2s(s\text{ - 20\rparen + 21\lparen s - 20\rparen = 0 } \\ (2s\text{ + 21\rparen\lparen s - 20\rparen = 0} \\ 2s\text{ + 21 = 0 or s - 20 = 0} \\ 2s\text{ = -21 or s = 20} \\ s\text{ = -21/2 or s = 20} \\ s\text{ = -10.5 or s = 20} \end{gathered}`

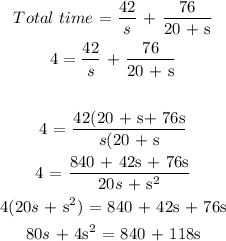
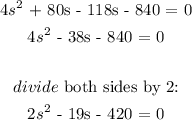
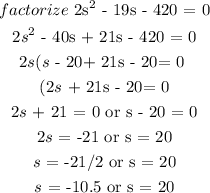
Since we can't have a negative number as speed, the speed will be 20 mph

The rate of speed of the motor boat is 20 mph