Question

Find the all solutions of this equation in the interval [0,2pi)2cos(x)+sqrt2=0

Answer 1

The given equation is:

`2\cos x+\sqrt[]{2}=0`

Move the constant to the right, changing its sign:

`\Rightarrow2\cos x=-\sqrt[]{2}`

Divide both sides of the equation by 2:

`\begin{gathered} (2\cos x)/(2)=\frac{-\sqrt[]{2}}{2} \\ \Rightarrow\cos x=\frac{-\sqrt[]{2}}{2} \end{gathered}`

Since cos t = cos(2π-t), it follows that the equation has two solutions:

`\cos x=-\frac{\sqrt[]{2}}{2};\; \cos \text{ (2}\pi-x)=-\frac{\sqrt[]{2}}{2}`

Consider the first equation:

`\begin{gathered} \cos x=-\frac{\sqrt[]{2}}{2} \\ Use\text{ the inverse trigonometry function to isolate x:} \\ \Rightarrow x=\arccos (-\frac{\sqrt[]{2}}{2}) \\ \Rightarrow x=(3\pi)/(4) \\ \end{gathered}`

Since the cosine function is periodic, add the period to the solution:

`\Rightarrow x=(3\pi)/(4)+2\pi k;\; k\in Z`

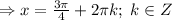
Consider the second equation and apply the same procedure as before:

`\begin{gathered} \; \cos \text{ (2}\pi-x)=-\frac{\sqrt[]{2}}{2} \\ \Rightarrow2\pi-x=(3\pi)/(4)+2\pi k \\ \Rightarrow-x=(3\pi)/(4)-2\pi+2\pi k \\ \Rightarrow-x=-(5\pi)/(4)+2\pi k \\ \Rightarrow x=(5\pi)/(4)-2\pi k \end{gathered}`

Since k is an integer, then -2πk=2πk.

`\Rightarrow x=(5\pi)/(4)+2\pi k`

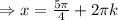
Hence the solutions are:

`\begin{cases}x=(3\pi)/(4)+2\pi k \\ x=(5\pi)/(4)+2\pi k\end{cases}k\in Z`

Notice that the solutions are required to be in [0,2π).

Hence, substitute integer values of k into the solutions and find values of x that fall in the given interval of solutions.

`\begin{gathered} x=(3\pi)/(4)+2\pi k;k=0 \\ \Rightarrow x=(3\pi)/(4)+2\pi(0)=(3\pi)/(4) \end{gathered}`

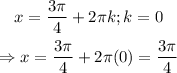
Other values of k will not fall in the required interval for this solution.

Check for the second solution:

`\begin{gathered} x=(5\pi)/(4)+2\pi k;k=0 \\ \Rightarrow x=(5\pi)/(4)+2\pi(0)=(5\pi)/(4) \end{gathered}`

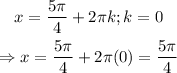
Other values for other integer values do not fall in the interval.

Hence, the solutions are:

`x=(3\pi)/(4),(5\pi)/(4)`