Step-by-step explanation
For a triangle with angles A, B and C and their corresponding opposite sides of lengths a, b and c the law of sines states the following:
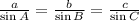
Before applying this law to our triangle it's important to recal another property of triangles. The sum of the 3 internal angles of a triangle is always 180°. If we use x for the missing angle we have the following equation for the triangle in the picture:
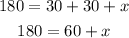
Then we substract 60 from both sides:
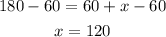
Now that we have the three angles we can apply the rule of sine to our problem. Using y and z for the two missing sides we get the following:
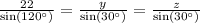
With this we can form two equations, one for y and another one for z:
![\begin{gathered} \frac{22}{\sin(120^{\operatorname{\circ}})}=\frac{z}{\sin(30^{\operatorname{\circ}})} \\ \begin{equation*} \frac{22}{\sin(120^{\operatorname{\circ}})}=\frac{y}{\sin(30^{\operatorname{\circ}})} \end{equation*} \end{gathered}]()
Let's start with the first equation. We can multiply both sides by the sine of 30°:
![\begin{gathered} \frac{22}{\sin(120^{\operatorname{\circ}})}\cdot\sin(30^{\operatorname{\circ}})=\frac{z}{\sin(30^{\operatorname{\circ}})}\cdot\sin(30^{\operatorname{\circ}}) \\ z=\frac{22}{\sin(120^{\operatorname{\circ}})}\cdot\sin(30^{\operatorname{\circ}})=(22)/(√(3)) \end{gathered}]()
Now we do the same with the second equation:
![\begin{gathered} \frac{22}{\sin(120^{\operatorname{\circ}})}\cdot\sin(30^{\operatorname{\circ}})=\frac{z}{\sin(30^{\operatorname{\circ}})}\cdot\sin(30^{\operatorname{\circ}}) \\ z=22\cdot\frac{\sin(30^{\operatorname{\circ}})}{\sin(120^{\operatorname{\circ}})}=(22)/(√(3)) \end{gathered}]()
So the two missing sides have a length of 22/√3 meters.
We then need to find the area of the triangle. The area of a triangle is given by the product of its base and its height divided by 2. In this case we can choose the 22 m side as the base so the height is the vertical distance between the base and its opposite angle. In order to find this height we can divide our triangle into two smaller right triangles:
The height we are looking for is the red segment h and the green segment is the half of the 22 m side so its length is 11 m. Then we can use the definition of the tangent in order to find h. In a right triangle, the tangent of an angle is given by the quotient between its opposite side and its adjacent side. Here h is the opposite side of the 30° angle and the green side is its adjacent side. Then we have the following equation:
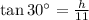
We multiply both sides by 11:
![\begin{gathered} \tg(30^{\operatorname{\circ}})\cdot11=(h)/(11)\cdot11 \\ h=11\tan30^(\circ)=(11)/(√(3)) \end{gathered}]()
Then the area of the triangle is:
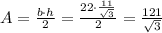
Then the area of the triangle is 121/√3 square meters.
Answers
a. The length of the missing sides is 22/√3 meters.
b. The area of the triangle is 121/√3 square meters.