The domain of the function represents all the values that the independent variable takes. The independent variable here is x, represented in the horizontal axis. We can see that the function can take any x-value since the parabola opens horizontally to both left and right indefinitely. That is why those two arrows are drawn. Then, the domain will be:
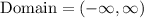
The part of an interval going to infinity (or minus infinity) is always open. That is why parenthesis are used instead of brackets.
The range of the function represents the values that the dependent variable can take. The dependent variable, in this case, is y, represented in the vertical axis. We can see that it does not take negative values, the graph extends vertically from the horizontal axis and up. Then, the range of the function contains values from 0 to infinity. The 0 is included because it is part of the graph. (-4+4)^2 = 0^2 = 0. Then, the range will be:
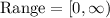
A bracket is used in 0 because it is a value that the y-vari