Question

A baseball player hits a ball. The table represents a quadratic function that shows how the height of the ball changes over time.Time (s) Height (ft)050.2580.5090.7581.0051.250Select from the drop-down menu to correctly complete the sentence.The y-coordinate of the vertex representsO the time, in seconds, that the ball is in the airO the maximum height, in feet, that the ball reaches O the height, in feet, when the ball hits the groundthe the time, in seconds, when the ball reaches its maximum height

Answer 1

The vertex is the maximum or minimum point of the equation's parabola

The general form of a quadratic equation is :

`\text{ y = ax}^2\text{ + bx + c}`

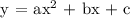
If we select the first two points i.e

`(0,\text{ 5) and (0.25, 8)}`

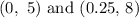
We substitute each point to get:

`5\text{ = c}`
`\begin{gathered} 8\text{ = 0.0625a + 0.25b + 5} \\ 0.0625a\text{ + 0.25b = 3 eqn (1)} \end{gathered}`

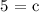
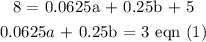
Select point (0.50, 9) and substitute into our general expression:

`\begin{gathered} 9\text{ = 0.25a + 0.5b + 5} \\ 0.25a\text{ + 0.5b = 4 eqn (2)} \end{gathered}`

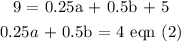
Solving eqn (1) and (2) simultaneously, we have

`\begin{gathered} a\text{ = -16} \\ b\text{ =16} \end{gathered}`

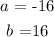
The quadratic equation is given as :

`H=-16t^2\text{ + 16t + 5}`

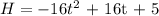
The x-coordinate of the vertex can be obtained as:

`\begin{gathered} =\text{ }(-b)/(2a) \\ =\text{ }\frac{-16}{2\text{ }*\text{ -16}} \\ =\text{ 0.5} \end{gathered}`

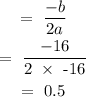
y-coordinate is obtained as :

`\begin{gathered} H=-16(0.5)^2\text{ + 16(0.5) + 5} \\ =\text{ 9} \end{gathered}`

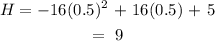
The correct option should be the time in seconds when the ball reaches the maximum height