Question

Help please! Kind of time sensitive I am having to turn all of my homework in I missed while being out due to medical reasons thank you!

Answer 1

Hello!

First, let's write some important information contained in the exercise:

• t = 0 (launching)

,

• h(t) = -4.9t² +250t +122

A)

We can solve it as a quadratic equation, equaling it to 0:

`-4.9t^(2)+250t+122=0`

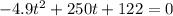
Let's find the coefficients:

• a = -4.9

,

• b = 250

,

• c = 122

Now, let's replace the values in the quadratic formula:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2\cdot a} \\ \\ x=\frac{-250\pm\sqrt[]{250^2-4\cdot(-4.9)\cdot122}}{2\cdot(-4.9)} \\ \\ x=\frac{-250\pm\sqrt[]{62500^{}+2391.2}}{-9.8} \\ \\ x=\frac{-250\pm\sqrt[]{64891.2}}{-9.8} \\ \\ x=(-250\pm254.7)/(-9.8) \\ \\ x^(\prime)=(-250-254.7)/(-9.8)=(-504.7)/(-9.8)=51.5 \end{gathered}`

Note: We don't need to calculate x'' because it will be negative, and we don't have a negative time.

B)

As the coefficient A is negative, it means that the concavity of the parabola will be facing downwards and this function will have a maximum point. So, let's use the formula below to obtain the height:

`\begin{gathered} X_M=(-b)/(2\cdot a)=(-250)/(2\cdot(-4.9))=(-250)/(-9.8)=25.51 \\ \\ Y_M=-(b^2-4\cdot a\cdot c)/(4\cdot a)=(250^2-4\cdot(-4.9)\cdot122)/(4\cdot(-4.9))=(64452)/(-9.8)=6576.73 \end{gathered}`

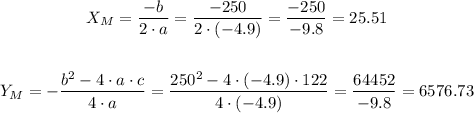
Answers:

The rocket splashes after 51.5 seconds.

The rocket peaks at 6,576.73 meters above sea level.