Question

What is the height at the peak of the projectiles trajectory if the magnitude vo equals 42.2 meters per second, and the angle ofΘis 41.8 degrees?

Answer 1

Take into account that the vertical final velocity of the projectile is given by:

`v^2_y=v^2_(oy)-2gy`

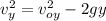
Now, consider that at the peak of the trajectory, the vertical final velocity is zero. Moreover:

`v^2_(oy)=v^2_o\sin ^2\theta`

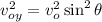
Then, by solving for y into the equation for vy^2, you obtain:

`\begin{gathered} o=v^2_o\sin ^2\theta-2gy \\ y=(v^2_o\sin \theta)/(2g) \end{gathered}`

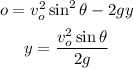
where g = 9.8m/s^2 is the gravitational acceleration constant.

By using the given values for the angle and vo you obtain for the height of the peak y:

`y=((42.2(m)/(s))(\sin 41.8)^2)/(2(9.8(m)/(s^2)))\approx40.36m`

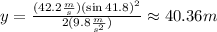
Hence, the height of the peak of the projectil trajectory is approximately 40.36 m