Answer:
24.24
Step-by-step explanation:
Sarah's composite score is the score such that:
P(X≤x) = 0.85
It means that the probability that a score will be lower than Sarah's score is 0.85.
But we have the standardized normal distribution table, so we first, will find a z such that:
P(Z≤z) = 0.85
Using the table, the closest number to 0.85 is 0.8508, so the value of z is 1.04.
1.0 from the row added to 0.04 from the column.
Now, x and z are related as:
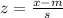
Where m is the mean and s is the standard deviation. So, replacing z by 1.04, m by 18, and s by 6, we get:
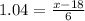
So, solving for x, we get:
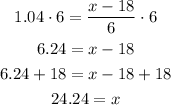
Therefore, Sarah's composite score is 24.24