Question

If Cody does a job in 87 hours and with the help of Patricia they can do it together in 58 hours, how long would it take Patricia to do it alone? hours

Answer 1

We can establish a "work rate" or velocity for Cody. It will represent the fraction of the job he does in an hour, or the "job per hour". If he does 1 job in 87 hours, it means that he does 1/87 of the job in an hour.

Similarly, when both Cody and Patricia work at the same time, they can do 1/58 of the job in an hour.

The combined job velocity (when they work together) is the sum of their individual velocities. Let's call P the velocity for Patricia:

`(1)/(87)+P=(1)/(58)`

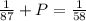
Now we can solve for P, which will give us the fraction of work Patricia is able to do in 1 hour:

`P=(1)/(58)-(1)/(87)=(87-58)/(5046)=(29)/(5046)`

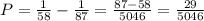
We can simplify the fraction, but for now, let's say Patricia does 29/5046 of the work in an hour. The time she would take to do the hob will be the inverse of that: 5046/29, which simplified gives us:

`\text{Time Patricia takes}=(5046)/(29)=(174)/(1)`

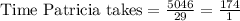
Then, Patricia will take 174 hours to do the job alone.