Question

The area (in square centimeters) of a square thank-you card can be representedby x2 + 6x + 9.a. Write an expression that represents the side length of the card.b. What is the perimeter of the card when x = 4?

Answer 1

a) The expression that represents the side length of the card = x + 3

b) The perimeter of the card when x is 4 = 28

Step-by-step explanation:
`a)\text{ Area of a square thank you card = x}^2\text{ + 6x + 9}`

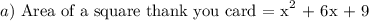
The formula for area of a square = length²

length = √area of the square

To find the length of the card, we will re-write the quadratic function into perfect square:

`\begin{gathered} \text{Area = }x^2\text{ + 6x + 9} \\ a\text{ = 1, b = 6, c = 9} \\ a\text{ }*\text{ c = 1 }*\text{ 9 = 9} \\ \text{factors of 9 whose sum gives 6: }3\text{ and 3} \\ 6x\text{ = 3x + 3x} \\ \\ x^2+6x+9=x^2\text{ + 3x + 3x + 9} \end{gathered}`
`\begin{gathered} \text{factorise x}^2\text{ + 3x + 3x + 9} \\ =x(x\text{ + 3) + 3(x + 3)} \\ =(x\text{ + 3)(x + 3)} \\ =(x+3)^2 \\ \\ \text{Area = }(x+3)^2 \end{gathered}`
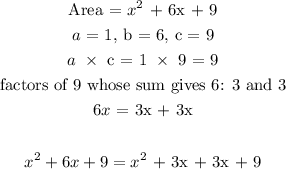
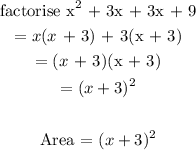
`\begin{gathered} \text{length = }\sqrt[]{area} \\ \text{length = }\sqrt[]{(x+3)^2} \\ \text{length = x + 3} \end{gathered}`

The expression that represents the side length of the card = x + 3

b) Perimeter of a square = 4(length of the side)

length of the side = x + 3

perimeter = 4(x + 3)

when x = 4

Perimeter = 4(4 + 3) = 4(7)

Perimeter = 28

The perimeter of the card when x is 4 = 28