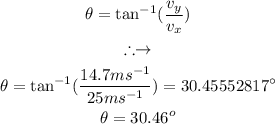Question

Jason Kendall throws a baseball with a horizontal component uf velocity of 25 m/s. It takes 3.00sto come back to its original height. Calculate its horizontal range, its initial vertical component ofvelocity and its initial angle of projection.

Answer 1

`\begin{gathered} s_x=75m \\ v_y=14.7ms^(-1) \\ \theta=30.46^o \end{gathered}`

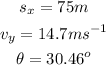
Step-by-step explanation: A baseball is thrown with some velocity, and it reaches the same height after 3.0s. the horizontal component of the velocity is 25m/s, we need to find (i) the range of the baseball (ii) the vertical component of the velocity, and (iii) the angle of the launch.

(i) Range of the baseball:

Since the range is the horizontal distance covered, and we know the horizontal velocity component and the total time of the flight, therefore the range can be calculated as follows:

`\begin{gathered} \text{Range }\Rightarrow s_x=v_xt \\ \therefore\rightarrow \\ s_x=(25ms^(-1))*_{}(3.0s)=75m \\ s_x=75m \end{gathered}`

(ii) The vertical component of the velocity:

For the vertical component of the velocity, we will resort to the equation of motion in the y-axis, from it we can solve for the vertical component of the velocity, this is done next:

`y(t)=y_o+v_yt-(1)/(2)gt^2\Rightarrow(1)`

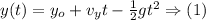
Using (1) and the fact that we have to set it equal to zero because the baseball lands at that height, the vertical velocity can be determined as follows:

`\begin{gathered} y(t)=y_o+v_yt-(1)/(2)gt^2\Rightarrow(1) \\ y_o=0 \\ t=3.0s \\ g=9.8ms^(-2) \\ \therefore\rightarrow \\ y_o+v_yt-(1)/(2)(9.8ms^(-2))t^2=0\Rightarrow v_y(3.0s)-(1)/(2)(9.8ms^(-2))*(3.0s)^2=0 \\ \therefore\rightarrow \\ v_y(3.0s)=(1)/(2)(9.8ms^(-2))*(3.0s)^2\Rightarrow v_y=(1)/(2)(9.8ms^(-2))(3.0s)=14.7ms^(-1) \\ v_y=14.7ms^(-1) \end{gathered}`

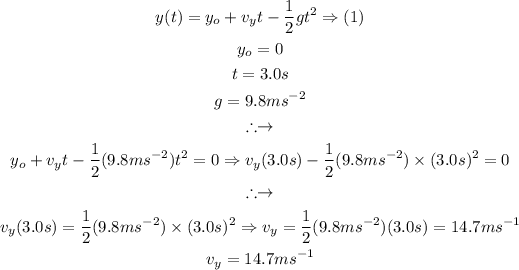
(iii) The angle of the launch:

The last step is to calculate the angle of the launch, this can be simply calculated as follows:

`\begin{gathered} \theta=\tan ^(-1)((v_y)/(v_x)) \\ \therefore\rightarrow \\ \theta=\tan ^(-1)(\frac{14.7ms^(-1)_{}}{25ms^(-1)})=30.45552817^(\circ) \\ \theta=30.46^o \end{gathered}`