First, use Newton's Second Law of Motion to find the acceleration of the object, given that its mass is 61.0kg and the force acting on it is 42.0N:
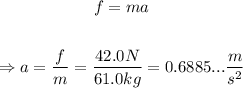
Next, remember that the distance d traveled while an object stops from an initial speed v under an acceleration a is given by:
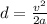
Replace v=23.0m/s and the value of the acceleration found above:
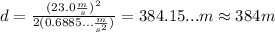
Therefore, the distance that it slides before coming to a stop is approximately 384m.