Given the function:
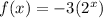
The function has the following domain:
{0, 1, 2, 3, 4}
Let's solve to find the smallest output.

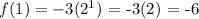
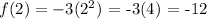

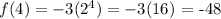
Therefore, the range/output of the function is:
{-3, -6, -12, -24, -48}
The smallest possible output of the function is -48
ANSWER:
-48