The number will have 5 slots. The first digit can be any odd digit from 0 to 9, then the first digit is one of the numbers in the set {1,3,5,7,9}, this means that we have 5 options. Now the last digit can't be the same as the first one but it has to be odd as well. then we have 4 options for the last slot.
Now from the second, third and fourth slots we can chosse any digit from 0 to 9 as long as it is not repeated then we have 8, 7 and 6 options. Then the total amount of 5 digit numbers with this specifications is:
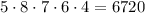
Now from this total the amount that starts with 3 is:
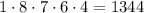
Therefore the probability is:

and this is equal to 0.2