Answer:
170 torr.
Step-by-step explanation:
To solve this problem we have to understand Dalton's Law: Dalton’s Law, or the Law of Partial Pressures, states that the total pressure exerted by a mixture of gases is equal to the sum of the partial pressures of the gases in the mixture.
The formula is the following:
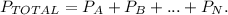
We have in this case, two solutions, so first, we have to calculate the total number of moles:
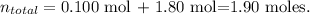
And now, let's calculate the mol fraction of each solution by dividing the moles of the certain substance by the total number of moles, like this:
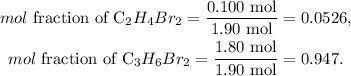
The next step is to calculate the vapor pressure of each substance by multiplying the mole fraction of each solution by its given pressure, like this:
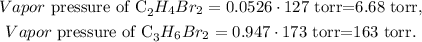
The final step is to sum the total vapor pressure by summing each vapor pressure of each substance:
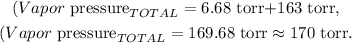
The answer would be that the total vapor pressure is 170 torr.