Question

In a certain country the heights of adult men are normally distributed with a mean of 66.5inches and a standard deviation of 2.5inches. The country's military requires that men have heights between 63inches and 73inches. Determine what percentage of this country's men are eligible for the military based on height.The percentage of men that are eligible for the military based on height is

Answer 1

91.458%

Explanation:

Given that the heights of adult men are normally distributed; and:

• The mean height = 66.5 inches

,

• The standard deviation = 2.5 inches.

We want to find the percentage that has heights between 63 inches and 73 inches.

In order to do this, we employ the use of the z-score formula.

`z=(X-\mu)/(\sigma)`

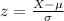
Thus:

`\begin{gathered} At\text{ X=63, }z=(63-66.5)/(2.5)=(-3.5)/(2.5)=-1.4 \\ At\text{ X=73, }z=(73-66.5)/(2.5)=(6.5)/(2.5)=2.6 \end{gathered}`

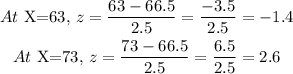
Next, using the z-score table:

[tex]P\mleft(-1.4Therefore, the percentage of men that are eligible for the military based on height is 91.458%.