ANSWER
T₂ = 10.19N
EXPLANATION
Given:
• The mass of the ball, m = 1.8kg
First, we draw the forces acting on the ball, adding the vertical and horizontal components of each one,
In this position, the ball is at rest, so, by Newton's second law of motion, for each direction we have,
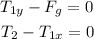
The components of the tension of the first string can be found considering that they form a right triangle, where the vector of the tension is the hypotenuse,

We have to find the tension in the horizontal string, T₂, but first, we have to find the tension 1 using the first equation,

Solve for T₁,
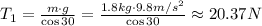
Now, we use the second equation to find the tension in the horizontal string,
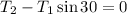
Solve for T₂,
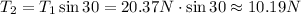
Hence, the tension in the horizontal string is 10.19N, rounded to the nearest hundredth.