Question

Hi, can you help me answer this question please, thank you!

Answer 1

The given information we have is:

significance level alfa=0.01

n=171

d=6.1

sd=39.8

To find the test statistic for this sample, let's calculate the z-score:

`\begin{gathered} Z=\frac{\bar{d}-\mu_d}{\sigma/\sqrt[]{n}} \\ Z=\frac{6.1-0}{39.8/\sqrt[]{171}} \\ Z=2.004 \end{gathered}`

The test statistic is 2.004.

The p-value has to be calculated as a two-tailed test, since the hypothesis Ha is ud is different to 0, which means can be greater or less than 0.

p-value for two tailed test is given by:

`\begin{gathered} p-\text{value}=P(Z\le-2.004)+P(Z\ge2.004) \\ p-\text{value}=P(Z\le-2.004)+(1-P(Z\le2.004) \\ p-value=0.0225+(1-0.977) \\ p-\text{value}=\text{0}.0225+0.0225 \\ p-\text{value}=\text{0}.0451 \end{gathered}`

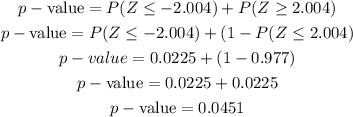
The p-value is 0.0451

The p-value is greater than alfa since 0.0451>0.01