Question

Given that Sin ∅ = -4/5 and Tan ∅ > 0, find Cos ∅ and Cot ∅

Answer 1

Trigonometry

We know that

`\begin{gathered} \tan \phi=(\sin\phi)/(\cos\phi)=(1)/(\cot\phi) \\ \cot \phi=(\cos\phi)/(\sin\phi)=(1)/(\tan\phi) \\ \sin ^2\phi+\cos ^2\phi=1 \end{gathered}`

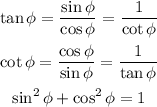
Using the third equation we are going to find cos∅:

`\begin{gathered} \sin ^2\phi+\cos ^2\phi=1 \\ \cos ^2\phi=1-\sin ^2\phi \\ \cos ^2\phi=1-(-(4)/(5))^2 \\ \cos ^2\phi=1-(16)/(25) \\ \cos ^2\phi=(9)/(25) \\ \cos \phi=\pm\sqrt[]{(9)/(25)} \\ \cos \phi=\pm(3)/(5) \end{gathered}`

We, have two possibilities cos∅ is positive or cos∅ is negative.

By the first equation and the given information Tan∅ > 0, we know that

`(\sin \phi)/(\cos \phi)>0`

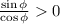
Since sin∅ is negative, and sin∅/cos∅ is positive, cos∅ must be negative so tan∅ > 0. Then

`\cos \phi=-(3)/(5)`

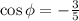
Using the second equation, we have that:

`\begin{gathered} \cot \phi=(\cos \phi)/(\sin \phi) \\ =(-(3)/(5))/(-(4)/(5))=(3)/(5)\cdot(5)/(4) \\ =(3)/(4) \end{gathered}`

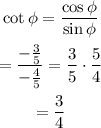
Answer: cos∅= -3/5 and cot∅​ = 3/4