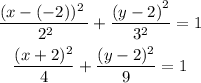Question

Can you please help me with 55For the following exercise given the graph of the ellipse determine its equation

Answer 1

`((x+2)^2\: )/(4)+((y-2)^2)/(9)=1`

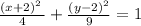
Explanation:

The general equation of an ellipse with no center at the origin is:

`(\mleft(x-h\mright)^2\: )/(\: a^2)+(\mleft(y-k\mright)^2)/(b^2)=1`

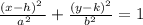
Where (h, k) is the center of the ellipse, a is the distance from the center to the edge horizontally, and b is the distance from the center to the edge vertically.

From the graph we obtain these values, just like this:

Therefore, the equation is:

`\begin{gathered} (\mleft(x-(-2)\mright)^2\: )/(\: 2^2)+(\left(y-2\right)^2)/(3^2)=1 \\ (\mleft(x+2\mright)^2)/(4)+(\mleft(y-2\mright)^2)/(9)=1 \end{gathered}`