We are given the following information
A child's piggy bank contains 44 coins in quarters and dimes.
Let q represents the number of quarters.
Let d represents the number of dimes.
Then the sum of q and d must be 44 coins.
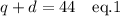
The coins have a total value of $8.60
We know that the worth of a quarter is 0.25 cents and the worth of a dime is 0.10 cents
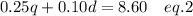
Now we have 2 equations and 2 unknowns so we can easily solve these equations using the substitution method.
From eq. 1 separate the value of d
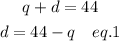
Now substitute this value into the eq.2
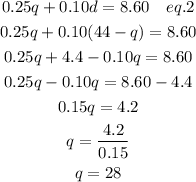
Therefore, the number of quarters in the bank are 28
(dimes are 44 - 28 = 16)