Question

If the circumference of a circle is increased by 50%, then its area will be increased by (a) 100% (b) 125% (c) 150% (d) 75%

Answer 1

Circumference is the distance around a plane shape. So, it also measures length.

Length and area of two similar shapes are related by the formula

`(A_1)/(A_2)=((l_1)/(l_2))^2`

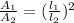
Where the A in both cases represents area and the L represents length. But here the Ls will represent circumference.

Since the circumference of the circle increased by 50%, then the new circumference becomes

`\begin{gathered} l_2=l_1+0.5l_1 \\ l_2=1.5l_1 \end{gathered}`

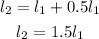
So, we have

`\begin{gathered} (A_1)/(A_2)=((l_1)/(l_2))^2 \\ (A_1)/(A_2)=(\frac{l_1}{1.5l_1_{}})^2 \\ (A_1)/(A_2)=\frac{l^2_1}{1.5^2l^2_1_{}} \\ (A_1)/(A_2)=(1)/(2.25) \end{gathered}`

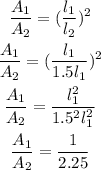
This becomes

`A_2=2.25A_1`

Now subtracting from the original area then

`2.25-1=1.25_{}`

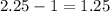
This means that the area was increased by 1.25, which means 125%

Hence option B is the correct answer