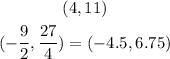Given the equation :

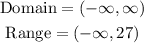
As it ascends during take-off, it makes a slanted line that cuts through the rainbow at two points.
See the following picture:
- Do all of the values make sense in this situation? Why or why not?
The answer is yes because the intersection between them will at two points
And one of them will be higher than the other
- What are the X- and y-intercepts of the rainbow?
As shown in the figure:
x-intercepts are the value when y = 0
So,
![\begin{gathered} y=0\rightarrow0=-x^2+27 \\ x^2=27 \\ x=\pm\sqrt[]{27}=\mleft\lbrace5.2,-5.2\mright\rbrace \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4u8zq7rikzqvhk5vlem0ss5re0gz5cknex.png)
So, x-intercepts are the points (-5.2, 0 ) and ( 5.2, 0 )
The Y-intercept is the value of y when x = 0
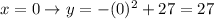
so, the y-intercept is the point ( 0, 27)
- Explain what each intercept represents in context.
The x-intercept is the value of x which make y = 0
The y-intercept is the value of y which make x = 0
- Is the linear function you created with your table positive or negative?
As shown in the figure: the linear function has a positive slope = 0.5
- What is the solution to the system of equations created?
The system of equations created are:
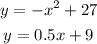
As shown in the figure, the solution of the system are the points: