Given the line
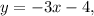
and the curve

in order to find the point at which they intersect, we must consider the equation:

Since this is a quadratic equation, let's move everything to the left side so that it equals 0. In other words, let's add 3x², 5x and subtract 2 from both sides:

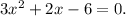
Let's solve this equation using the general formula for quadratic equations:
![x=\frac{-2\pm\sqrt[]{4-4(3)(-6)}}{2(3)},](https://img.qammunity.org/2023/formulas/mathematics/college/x1m9tmg554dnadkw1u9la18vxxt3ipwtlz.png)
![x=\frac{-2\pm\sqrt[]{4+72}}{6},](https://img.qammunity.org/2023/formulas/mathematics/college/yb0lyokdqmglr69mfkeei0ubh3ef780s7s.png)
![x=\frac{-2\pm\sqrt[]{76}}{6},](https://img.qammunity.org/2023/formulas/mathematics/college/4vtwhyv8wx6210k9otkt6mqbx7a1wifabb.png)
![x=\frac{-2\pm2\cdot\sqrt[]{19}}{6}\text{.}](https://img.qammunity.org/2023/formulas/mathematics/college/ysuwrk6jj3plo3oofdvd2k4jxan83rof7i.png)
This gives us the following two values of x:
![x=-(1)/(3)+(1)/(3)\cdot\sqrt[]{19},](https://img.qammunity.org/2023/formulas/mathematics/college/9qxp0v5brhv3z71vqkimfb8ru1imzl1c3h.png)
and
![x=-(1)/(3)-(1)/(3)\cdot\sqrt[]{19}.](https://img.qammunity.org/2023/formulas/mathematics/college/hkpoblvsbi5c4g7sr1ungq238mzxwqbp5x.png)
Now we know the x-coordinate of the points of intersection. In order to get the y-coordinate, we substitute these values on either of the equations we were given to begin with. We'll do it on the line since it's easier:
On one hand:
![y=-3(-(1)/(3)+(1)/(3)\cdot\sqrt[]{19})-4=1-\sqrt[]{19}-4=-3-\sqrt[]{19},](https://img.qammunity.org/2023/formulas/mathematics/college/dwzazdc6ku0cb41brwg7zgryea30qi4jnu.png)
on the other:
![y=-3(-(1)/(3)-(1)/(3)\cdot\sqrt[]{19})-4=1+\sqrt[]{19}-4=-3+\sqrt[]{19}.](https://img.qammunity.org/2023/formulas/mathematics/college/8g6694r9vy244v2o8rmcs7vbkmshaxezir.png)
So the points of intersection are
![(-(1)/(3)+(1)/(3)\cdot\sqrt[]{19},-3-\sqrt[]{19}),](https://img.qammunity.org/2023/formulas/mathematics/college/p1gu3s7tuud1yw5o6yz8zfcokq2mu5mj7w.png)
and
![(-(1)/(3)-(1)/(3)\cdot\sqrt[]{19},-3+\sqrt[]{19}).](https://img.qammunity.org/2023/formulas/mathematics/college/g0si9l11svarvuve6dbr3fzvfyrbps0qwn.png)
In the image, we can see the approximate values of these coordinates.