Question

Find the area of the figure below Braun your answer to one decimal place

Answer 1

To determine the area of the figure you have to decompose it into two simpler figures:

A semicircle (green) and a rectangle (blue)

The total area of the figure is equal to the area of the semicircle plus the area of the rectangle

`A_T=A_C+A_R`

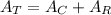
The area of the rectangle can be calculated as

`\begin{gathered} A_R=w\cdot l \\ A_R=6\cdot12 \\ A_R=72 \end{gathered}`

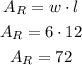
The area of a circle can be calculated as

`\text{Acircle}=\pi r^2`

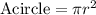
To calculate the area of the semicircle you have to divide it by 2

`A_C=(\pi r^2)/(2)`

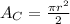
The semicircle has a diameter of d=6

So the radius is

`r=(d)/(2)=(6)/(2)=3`

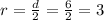
The area of the semicircle is

`\begin{gathered} A_C=(\pi r^2)/(2) \\ A_C=(\pi3^2)/(2) \\ A_C=(9)/(2)\pi \end{gathered}`

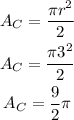
Finally add both areas to determine the area of the figure

`\begin{gathered} A_T=A_R+A_C \\ A_T=72+(9)/(2)\pi \\ A_T=86.137\cong86.1 \end{gathered}`

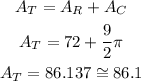
The total area of the figure is 86.1