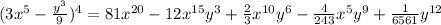Question

I need help solving this, it’s from my trigonometry prep bookIt asks to answer (a) and (b)Please put these ^ separately so I know which is which

Answer 1

`\begin{gathered} (a)\sum ^4_{k\mathop{=}0}\begin{bmatrix}{} & 4 \\ {} & {k}\end{bmatrix}(3x^5)^(4-k)(-(1)/(9)y^3)^k \\ (b)81x^(20)-12x^(15)y^3+(2)/(3)x^(10)y^6-(4)/(243)x^5y^9+(1)/(6561)y^(12) \end{gathered}`

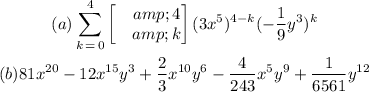
Step-by-step explanation

We want to expand the given expression using binomial expansion:

`(3x^5-(1)/(9)y^3)^4`

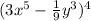
(a) In summation notation, binomial expansion is written as:

`(a+b)^n=\sum ^n_(k\mathop=0)\begin{bmatrix}{} & n \\ {} & {k}\end{bmatrix}a^(n-k)b^k`

where:

`\begin{gathered} a=3x^5 \\ b=-(1)/(9)y^3 \\ n=4 \end{gathered}`

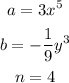
Therefore, the summation notation for the expansion is:

`(3x^5-(1)/(9)y^3)^4=\sum ^4_{k\mathop{=}0}\begin{bmatrix}{} & 4 \\ {} & {k}\end{bmatrix}(3x^5)^(4-k)(-(1)/(9)y^3)^k`

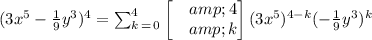
(b) Now, we want to expand the expression. To do this, find each term taking k to go from 0 to 4, find the sum of the terms, and simplify.

That is:

`\begin{gathered} k=0\colon \\ ^{}\begin{bmatrix}{4} & {} \\ {0} & {}\end{bmatrix}(3x^5)^(4-0)(-(y^3)/(9))^0 \\ (4!)/((4-0)!0!)(3x^5)^4 \\ \Rightarrow81x^(20) \end{gathered}`
`\begin{gathered} k=1\colon \\ \begin{bmatrix}{4} & {} \\ {1} & {}\end{bmatrix}(3x^5)^(4-1)((-y^3)/(9))^1_{} \\ (4!)/((4-1)!1!)(3x^5)^3((-y^3)/(9)) \\ \Rightarrow-12x^(15)y^3 \end{gathered}`
`\begin{gathered} k=2\colon \\ \begin{bmatrix}{4} & {} \\ {2} & {}\end{bmatrix}(3x^5)^(4-2)(-(y^3)/(9))^2 \\ (4!)/((4-2)!2!)(3x^5)^2(-(y^3)/(9))^2 \\ \Rightarrow(2)/(3)x^(10)y^6 \end{gathered}`
`\begin{gathered} k=3\colon \\ \begin{bmatrix}{4} & {} \\ {3} & {}\end{bmatrix}(3x^5)^(4-3)(-(y^3)/(9))^3 \\ (4!)/((4-3)!3!)(3x^5)(-(y^3)/(9))^3 \\ \Rightarrow-(4)/(243)x^5y^9 \end{gathered}`
`\begin{gathered} k=4\colon \\ \begin{bmatrix}{4} & {} \\ {4} & {}\end{bmatrix}(3x^5)^(4-4)(-(y^3)/(9))^4 \\ (4!)/((4-4)!4!)(-(y^3)/(9))^4^{} \\ (1)/(6561)y^(12) \end{gathered}`

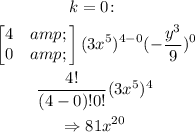
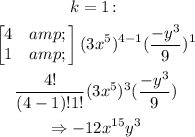
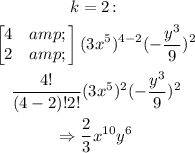
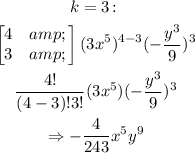
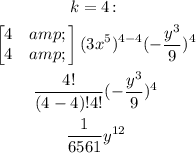
Therefore, in simplified form, the expanded expression is:

`(3x^5-(y^3)/(9))^4=81x^(20)-12x^(15)y^3+(2)/(3)x^(10)y^6-(4)/(243)x^5y^9+(1)/(6561)y^(12)`