Question

INSTRUCTIONS: INSTRUCTIONS: NS: of the line ere: m=2 Find the slope of the line and enter it here: Find the slope of the line and enter it here: 2. tercept of ter it Find the y-intercept of the line & enter it here: Find the y-intercept of the line & enter it here: 3. Write the equation of the line in formy=mx +b Write the equation of the line in form y=mx+b quation of orm y=mx +b -3 23 24 3 o

Answer 1

Point 1. To find the slope of the line you can use the following formula:

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \text{ Where m is the slope of the line and} \\ (x_1,y_1)\text{ and}(x_2,y_2)\text{ are two points through which the line passes} \end{gathered}`

If for example, you take the ordered pairs (-4,3) and (-2,4) you have

`\begin{gathered} (x_1,y_1)=(-4,3) \\ (x_2,y_2)=(-2,4) \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(4-3)/(-2-(-4)) \\ m=(1)/(-2+4) \\ m=(1)/(2) \end{gathered}`

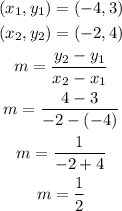
Therefore, the slope of the line is 1/2.

Points 2 and 3. You can use the point-slope formula to find the y-intercept and to find the equation of the line in its form y = mx + b

`\begin{gathered} y-y_1=m(x-x_1)\Rightarrow\text{ Point-slope formula} \\ y-3_{}=(1)/(2)(x-(-4)) \end{gathered}`

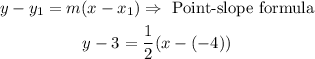
Now, solve for y

`\begin{gathered} y-3_{}=(1)/(2)(x+4) \\ \text{ Apply distributive property} \\ y-3_{}=(1)/(2)x+4\cdot(1)/(2) \\ y-3_{}=(1)/(2)x+2 \\ \text{ Add 3 from both sides of the equation} \\ y-3_{}+3=(1)/(2)x+2+3 \\ y=(1)/(2)x+5 \end{gathered}`

Then, you have

`\begin{gathered} y=mx+b \\ \text{ Where m is the slope of the line and} \\ \text{b is the y-intercept} \end{gathered}`

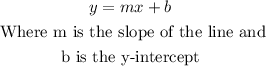
Therefore, the equation of the line in its form y = mx + b is

`y=(1)/(2)x+5`

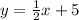
And the y-intercept is 5. Also, you can see that the line intersects the y-axis at y = 5, which confirms that the y-intercept is 5.