Question

Find the indicated sides to the nearest thousandths and angles to the nearest degree. YOU MUST SETUP EQUATION AND SOLVE sin rule

Answer 1

Using Law of Sines

`(\sin(A))/(a)=(\sin(B))/(b)=(\sin (C))/(c)`

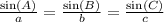
The Law of Sines states that there is a proportional relationship between the angles and sides of an oblique triangle.

We see that we have two angles that we need to solve, and can label our triangle as such:

The angles are capital A, B, and C, whereas our sides are lowercase a, b, and c.

We need to find the angles first, and we can do so with our knowledge of one angle and the side directly across from it. We know both capital C and lowercase c, so let's create a proportion.

`\begin{gathered} (\sin(C))/(c)=(\sin (B))/(b) \\ (\sin(90))/(8)=(\sin (B))/(4) \end{gathered}`

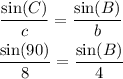
When we create a proportion, we cross-multiply our values.

`4\sin (90)=8\sin (B)`

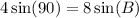
We need to get B by itself since that is what we are solving for.

`\begin{gathered} (4\sin(90))/(8)=(8\sin (B))/(8) \\ (4\sin(90))/(8)=\sin (B) \\ \sin (B)=(4\sin(90))/(8) \end{gathered}`

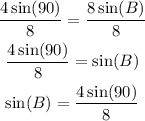
Now, we use the inverse of sin, plug in the value, and solve for sin(B). You'll need a calculator for this part.

`\sin ^(-1)((4\sin(90))/(8))=30`

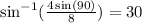
This gives us the value for angle B, or angle y in the given diagram.

Now, we can simply add our two solved angles together and subtract them from 180 to find our third angle.

`\begin{gathered} 90+30=120 \\ 180-120=60 \end{gathered}`

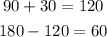
This means that our angle x is 60 degrees.

Finally, we need to set up one last proportion to find a, or the side adjacent to the right angle and vertical.

`\begin{gathered} (\sin(C))/(c)=(\sin (A))/(a) \\ (\sin(90))/(8)=(\sin (30))/(a) \end{gathered}`

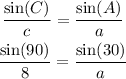
Once again, we cross multiply:

`a\sin (90)=8\sin (30)_{}`

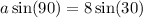
Then, we need to get a by itself.

`\begin{gathered} (a\sin(90))/(\sin(90))=(8\sin (30))/(\sin (90)) \\ a=(8\sin(30))/(\sin(90)) \end{gathered}`

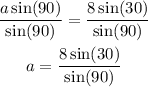
Then, we divide the two values and solve for a. Use a calculator and plug it in to solve.

`(8\sin (30))/(\sin (90))=4`

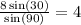
Therefore, side a equals 4.

Our triangle will look like this:

Therefore, this is the final answer.

The angles are:

90 degrees

x = 30 degrees

y = 60 degrees

The sides are:

8 units

4 units

Unknown side = 4 units