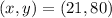Question

The drama club is selling tickets to their play to raise money for the show's expenses. Each student ticket sells for $5 and each adult ticket sells for $9.50. The auditorium can hold at most 110 people. The drama club must make a minimum of $760 from ticket sales to cover the show's costs. Also, they must sell at least 20 student tickets. If x x represents the number of student tickets sold and y y represents the number of adult tickets sold, write and solve a system of inequalities graphically and determine one possible solution.

Answer 1

According to the given problem, there are 'x' student tickets and 'y' adult tickets.

Given that there must be at least 20 student tickets,

`x\ge20`

The auditorium can hold a maximum of 110 people, so the number of tickets sold must not exceed this limit,

`x+y\leq110`

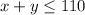
If a student ticket costs $5 and an adult ticket costs $9.50, then the total cost of 'x' student tickets and 'y' adult tickets, is given by,

`=5x+9.5y`

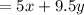
Given that this cost must be $760 or more,

`5x+9.5y\ge760`

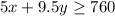
So the system of inequalities is obtained as,

`\begin{gathered} 5x+9.5y\ge760 \\ x+y\leq110 \\ x\ge20 \end{gathered}`

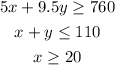
Since 'x' and 'y' are the number of tickets, they must always be positive, and the non-negativity constraints must be followed,

`\begin{gathered} x\ge0 \\ y\ge0 \end{gathered}`

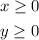
Consider that all the above inequalities are linear. So the boundary of the enclosed region will be lines as given by the corresponding equations,

`\begin{gathered} 5x+9.5y=760 \\ x+y=110 \\ x=20 \end{gathered}`

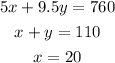
The first line passes through the points (0,80) and (152,0). The second line passes through the points (110,0) and (0,110). And the third line is vertical at x=20.

Note that the first equation and third equation does not satisfy the coordinates of the origin, so the region not containing origin will be the solution region for each of these two inequalities. The coordinates of the origin satisfy the second inequality, so the region containing origin will be the region for this particular inequality.

And the region common to all the three inequalities will be the solution region for the system of inequalities.

The corresponding graph is given below,

Thus, the solution region is obtained as the triangular area ABC.

It is asked to determine a possible solution to the given problem. For this, we randomly pick a point just left to the line AB that could lie in the region ABC, and finally check if that point satisfies the system of inequality.

Let us check for the point (21,80), that is,

`(x,y)=(21,80)`

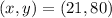
Check for each inequality of the system.

Consider the first inequality,

`\begin{gathered} 5(21)+9.5(80)\ge760 \\ 105+760\ge760 \\ 865\ge760 \end{gathered}`

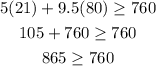
The result obtained is true, so the point satisfies the first inequality.

Consider the second inequality,

`\begin{gathered} (21)+(80)\leq110 \\ 101\leq110 \end{gathered}`

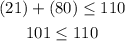
The result obtained is true, so the point satisfies the second inequality.

Consider the third inequality,

`\begin{gathered} (21)\ge20 \\ 21\ge20 \end{gathered}`

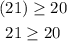
The result obtained is true, so the point satisfies the third inequality.

Since all the three inequalities of the system are satisfied, the point (21,80) must be a solution of the system.

Therefore, one possible solution of the system of inequalities is,

`(x,y)=(21,80)`