Question

Find the term that must be added to the equation X 2- 6r = 7 to make it into a perfect square.

Answer 1

In this problem, we have to complete the square for a quadratic equation.

Recall that a perfect square trinomial comes in the form:

`a^2+2ab+b^2`

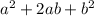
Sometimes, we have to create that form by using the following method to complete the square:

1. Get the equation equal to

`ax^2+bx=-c`

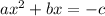
2. Divide the b-term and square it:

`((b)/(2))^2`

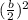
3. Add that new value to both sides of the equation:

`ax^2+bx+((b)/(2))^2=-c+((b)/(2))^2`

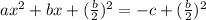
It looks really confusing in this format, so let's follow our equation to get a better idea.

We are given:

`x^2-6x=7`

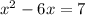
Luckily, we already have it in the format required for Step 1. So we can complete Step 2 by identifying the b-value.

`\begin{gathered} x^2-6x=7 \\ \\ \text{ The b-value is:}b=-6 \end{gathered}`

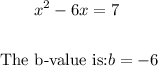
So, we have:

`((-6)/(2))^\rightarrow(-3)^(^2)\rightarrow9`

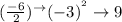
Finally for Step 3, we add that 9 to both sides to get:

`\begin{gathered} x^2-6x+9=7+9 \\ \\ x^2-6x+9=16 \end{gathered}`

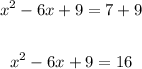
The term tha tmust be added to the equation to make it into a perfect square is 9.