We are given the following inequality:

To solve for "x" we will add 2x to both sides:
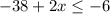
Now we will add 38 to both sides:
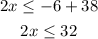
Now we divide both sides by 2:
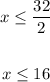
Therefore, the solution is the values of "x" that are smaller or equal to 16. This can be represented in the real line as follows:
We need to use all the points that are smaller (to the left) than 16. To represent the fact that 16 is also included in the solution we use a point on top of it.
In the case that 16 was not included then we would use a hollowed point on top of it.