Question

The height of a triangle is three more than two times the base. The area of the triangle is 45 square feet. What are the dimensions of the triangle?

Answer 1

Let us set H for the height and b for the base:

H= three more than two times the base.

Then

H = 3+2b

Now, the area of the triangle is 45 feet square.

The area is given by the next formula:

`A=(b\ast h)/(2)`

Then, we can replace

A = 45

H = 3+2b

`45=(b(3+2b))/(2)`

Solve for b

`\begin{gathered} 3b+2b^2=2\ast45 \\ 2b^2+3b-90=0 \end{gathered}`

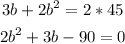
Use the quadratic equation:

`b=(-b\pm√(b^2-4ac))/(2a)`

Use the form ax²+bx+c:

Where a=2, b=3 and c=-90

Replacing:

`\begin{gathered} b=(-3\pm√((-3)^2-4(2)(-90)))/(2(2)) \\ Simplify: \\ b=6 \end{gathered}`

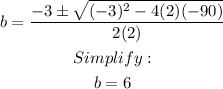
Hence, the base is equal to 6 feet.

Then:

H =3+2b

Replace b=6

H=3+2(6)

H = 15

Therefore, the height of the triangle is equal to 15 feet