Step-by-step explanation
We define the following sets:
• C = athletes that have a convertible,
,
• T = athletes that have a giant TV screen,
,
• S = athletes that have a sporting goods store,
,
• U = all the athletes of the survey.
We denote n(A) as the number of items inside set A, one of the sets C, T or S.
To answer the questions, we will use the following Venn diagram of the sets:
From the statement, we know that:
• n(U) = 277,
,
• n(C) = 146,
,
• n(T) = 128,
,
• n(S) = 117,
,
• n(C ∩ S) = 31,
,
• n(T ∩ S) = 47,
,
• n(C ∩ T) = 74,
,
• n(C ∩ T ∩ S) = 14.
1) How many athletes did not own any of the three items?
Using the Venn, we see that this number is equal to the number of items in U that are not in C ∩ T ∩ S, so we have:

2) How many owned a convertible and a TV, but not a store?
Using the Venn, we see that this number is equal to the number of items in C ∩ T minus the ones in C ∩ T ∩ S:
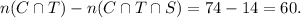
3) How many athletes owned a convertible or a TV?
Using the Venn, we see that this number is equal to the number of items in the set C U T, which is given by:
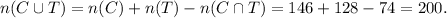
4) How many athletes owned exactly one type of item in the survey?
Using the Venn, we must sum the number of athletes that are only in C, plus the items only in T, plus the items only in S:
![\begin{gathered} n(only\text{ }C)=n(C)-n(C\cap T)-n(C\cup S)+(C\cap T\cap S)=277-74-31+14=186, \\ n(only\text{ }T)=n(T)-n(T\operatorname{\cap}C)-n(T\cap S)+n(C\operatorname{\cap}T\operatorname{\cap}S)=128-74-47+14=21, \\ n(only\text{ }S)=n(S)-n(S\operatorname{\cap}C)-n(S\operatorname{\cap}T)+n(C\operatorname{\cap}T\operatorname{\cap}S)=117-31-47+14=25. \end{gathered}]()
So the number of athletes that has only one item is given by the sum of these numbers:
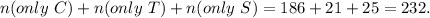
5) How many athletes owned at least one type of item in the survey?
This number is given by the sum of elements in the set C U T U S:
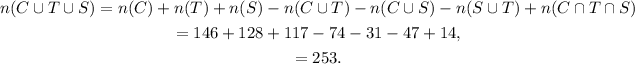
6) How many owned a TV or a store, but not a convertible?
Using the Venn, we see that this number is equal to the number of items in T ∩ S minus the ones in C ∩ T ∩ S:
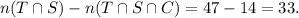
Answer
1) 263
2) 60
3) 200
4) 232
5) 253
6) 33