Question

I only need these 5 points. the vertex, 2 to the left of it, 2 to the right of it.

Answer 1

First, let us find the vertex of the parabola. In a given equation:

`y=a(x-h)^2+k`

The vertex is found at (h,k)

Now, from our equation:

`\begin{gathered} y=(x+4)^2-2 \\ h=-4 \\ k=-2 \end{gathered}`

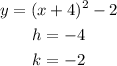
Therefore, the vertex is at (-4, -2).

Then, let us find the x-intercepts of the parabola by equating the equation to 0.

`\begin{gathered} y=(x+4)^2-2 \\ 0=(x+4)^2-2 \\ 0=x^2+8x+16-2 \\ x^2+8x+14=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}_{}}{2a} \\ x=\frac{-8\pm\sqrt[]{8^2-4(1)(14)}_{}}{2(1)} \\ x=\frac{-8\pm\sqrt[]{64+56}_{}}{2} \\ x=\frac{-8\pm\sqrt[]{8}_{}}{2} \\ x=\frac{-8\pm2\sqrt[]{2}_{}}{2} \\ x=-4+\sqrt[]{2}=-2.59 \\ x=-4-\sqrt[]{2}=-5.41 \end{gathered}`

Since the values gave us decimal values, let us try to find the y-values using a table of values for x.

`\begin{gathered} y=(x+4)^2-2 \\ y=((-2)+4)^2-2=2 \\ y=((-1)+4)^2-2=7 \\ y=((-6)+4)^2-2=2 \\ y=((-7)+4)^2-2=7 \end{gathered}`

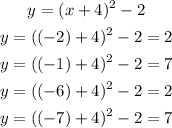
With this, we now have the points:

(-2,2)

(-1,7)

(-6,2)

(-7,7)

And the vertex (-4,-2)

The graph would look like this: