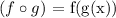Question:
Solution:
By definition we have that:
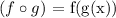
On the other hand, it is not always true that
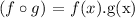
In fact, the only case in which the above occurs is when f (x) = g (x) = 1
Thus, we can conclude that the correct answer is:
The statement is not true for all pairs of functions. A statement that is true for every f(x) and g(x) is