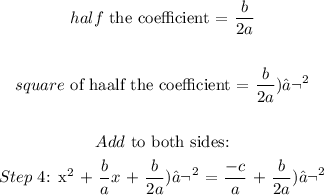Question

The steps to derive the quadratic formula are shown below:Step 1ax2 + bx + c = 0Step 2ax2 + bx = − cStep 3x2 + b over a times x equals negative c over aStep 4Provide the next step to derive the quadratic formula.

Answer 1

Answer:
`\text{x}^2\text{ + }(b)/(a)x\text{ + \lparen}(b)/(2a))\placeholder{⬚}^2\text{ = }(-c)/(a)\text{ + \lparen}(b)/(2a))\placeholder{⬚}^2\text{ \lparen2nd option\rparen}`

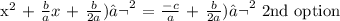
Step-by-step explanation:

Given:

The steps to derive the quadratic formula

To find:

step 4 of the process

`\begin{gathered} Step\text{ }1:\text{ }ax^2+bx+c=0 \\ Step\text{ }2:\text{ }ax^2+bx=−c \\ Step\text{ 3: x}^2\text{ + }(bx)/(a)\text{ = }(-c)/(a) \end{gathered}`

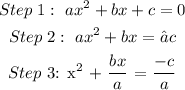
To get step 4, we will apply the complete square method. We will add the square of half the coefficient of x to both sides of the equation

coefficient of x = b/a

half the coefficient = 1/2 (b/a)

`\begin{gathered} half\text{ the coefficient = }(b)/(2a) \\ \\ square\text{ of haalf the coefficient = \lparen}(b)/(2a))\placeholder{⬚}^2 \\ \\ Add\text{ to both sides:} \\ Step\text{ 4: x}^2\text{ + }(b)/(a)x\text{ + \lparen}(b)/(2a))\placeholder{⬚}^2\text{ = }(-c)/(a)\text{ + \lparen}(b)/(2a))\placeholder{⬚}^2 \end{gathered}`