Question

A mass of 0.520 kilograms is attached to a spring and lowered into a resting position, causing the spring to stretch 18.7 centimeters. The mass is then lifted up and released. What is the frequency of its oscillation? Include units in your answer. Answer must be in 3 significant digits.

Answer 1

Given,

The mass attached to the spring, m=0.520 kg

The stretching of the spring, x=18.7 cm=0.187 m

The restoring force of spring is given by,

`F=kx`

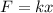
Where k is the spring constant of the spring.

The force F is equal to the weight of the mass attached.

Thus,

`\begin{gathered} F=mg=kx \\ \Rightarrow k=(mg)/(x) \end{gathered}`

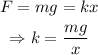
Where g is the acceleration due to gravity.

On substituting the known values,

`\begin{gathered} k=(0.520*9.8)/(0.187) \\ =27.3\text{ N/m} \end{gathered}`

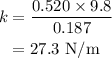
The frequency of the spring is given by,

`f=(1)/(T)=(1)/(2\pi)\sqrt[]{(k)/(m)}`

where T is the period of oscillation of spring.

On substituting the known values,

`\begin{gathered} f=(1)/(2\pi)\sqrt[]{(27.3)/(0.520)} \\ =1.15\text{ Hz} \end{gathered}`

Thus the frequency of oscillation of the spring is 1.15 Hz.