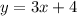Question

Find an equation for the perpendicular bisected of the line segment whose endpoints are (3,-7) (-9,-3).

Answer 1

To find the perpendicular bisected of the line segment whose endpoints are (3,-7) (-9,-3).​

We need to things:

1. the midpoint of the given point

2. the slope

The midpoint = p

`p=((3,-7)+(-9,-3))/(2)=((-6,-10))/(2)=(-3,-5)`

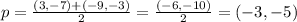
To find the slope, first we will find the slope of the line segment whose endpoints are

(3,-7) (-9,-3)

so,

Slope = m = rise/run

Rise = -3 - (-7) = 4

Run = -9 - 3 = -12

Slope =

`m=(4)/(-12)=-(1)/(3)`

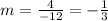
The slope of the required line = m'

`m^(\prime)=-(1)/(m)=-(1)/((-1)/(3))=3`

So, the equation of the line will be :

`y=3x+b`

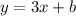
b is the y - intercept and will be calculated using the point p

when x = -3 , y = -5

so,

`\begin{gathered} -5=3\cdot-3+b \\ -5=-9+b \\ b=-5+9 \\ b=4 \end{gathered}`

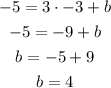
So, the equation for the perpendicular bisected is:

`y=3x+4`