The function of the height is,
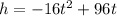
where,
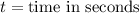
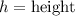
We will start substituting the values of t starting from when t= 0 till the function gives us negative.
Step 1:
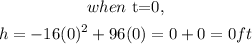
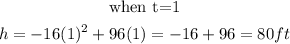
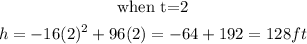
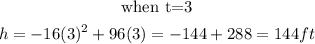
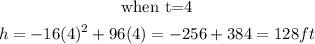
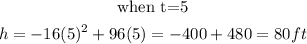
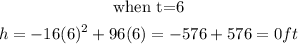
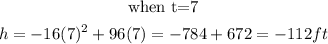
Step 2:
Step 3: We are to plot the graph and determine the highest point.
Hence, from the graph we can confirm that the time in which the projectile was in the air is 6seconds.