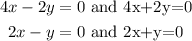Question

What are the vertices, foci, and asymptotes of the hyperbola with the equation 16x^2 - 4y^2 = 64show the steps

Answer 1

Given the equation of the hyperbola

`16x^2-4y^2=64`

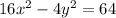
The standard equation of hyperbola is of the form

`(x^2)/(a^2)-(y^2)/(b^2)=1`

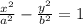
Write the given equation of hyperbola in standard form.

Divide the given equation by 64.

`\begin{gathered} (16x^2)/(64)-(4y^2)/(64)=1 \\ (x^2)/(4)-(y^2)/(16)=1 \end{gathered}`

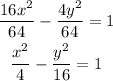
Comparing with the standard form gives

`a=2,b=4`

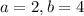
Vertices are

`\begin{gathered} =(\pm a,0) \\ =(\pm2,0) \end{gathered}`

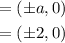
Find the eccentricity.

`\begin{gathered} e=\frac{\sqrt[]{a^2+b^2}}{a} \\ =\frac{\sqrt[]{4+16}}{2} \\ =\frac{\sqrt[]{20}}{2} \\ =\sqrt[]{5} \end{gathered}`

Foci are

`\begin{gathered} =(\pm ae,0) \\ =(\pm2\sqrt[]{5},0) \end{gathered}`

Asymptotes are bx-ay = 0 and bx+ay=0

`\begin{gathered} 4x-2y=0\text{ and 4x+2y=0} \\ 2x-y=0\text{ and 2x+y=0} \end{gathered}`