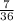To find the probability of getting a sum of 3 or 8:
It is given that,
Two dice are rolled.
So, the total sample space, n(s)=36.
A be the event of getting a sum of 3.
So, A={(1,2), (2,1)}
n(A)=2
B be the event of getting a sum of 8.
So, B={(2,6), (3,5), (4,4), (5,3), (6,2)}
n(B)=5.
n(AnB)=0.
Using the formula,
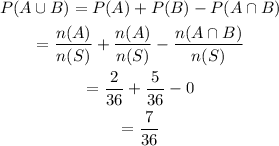
Hence, the answer is,