Question

efgh is rotated 90 degrers clockwise about the origin and then translate it 3 units down if the coordinates of a resultant point is 1,-4 what were the coordinates original point?A. 2,5B.4,5C.3,1D.1,1

Answer 1

90-degree clockwise rotation transforms the coordinates the following way:

`(x,y)\rightarrow(y,-x)`

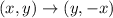
Now, after performing 90-degree clockwise rotation, we also move our point 3 units down, meaning, the final coordinates of the point are

`(y,-x-3)`

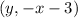
Now we are told that the coordinates of the resultant point are

`(1,-4)`

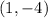
meaning

`\begin{gathered} y=1 \\ -x-3=-4 \\ \end{gathered}`

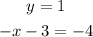
Solving for x gives

`\begin{gathered} y=1 \\ x=1 \end{gathered}`

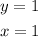
Hence, the coordinates of the original point are

`(1,1)`

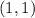
which is choice D.