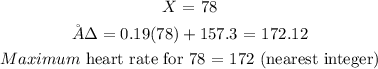1) y = 0.19X + 157.3 (option C)
2) Yes, it is a good fit
3) i) 165
ii) 168
iii) 172
Step-by-step explanation:
1)2) Regression equation is given as:
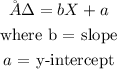
To determine the regression equation, we will use a regression calculator:
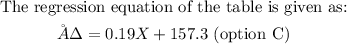
2) The correlation coefficient = r = 0.98510411
A correlation coefficient that is close to 1 is a strong correlation and it makes it a good fit.
Yes, it is a good fit
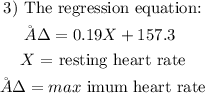
To get the maximum heart rate for a resting heart, we will substitute X with the values given
For resting heart rate of 42:
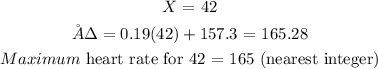
For resting heart rate of 57:
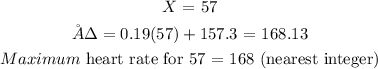
For resting heart rate of 78: