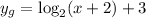Question

Asymptotes are when a function gets close to an imaginary line. A horizontal asymptote means the imaginary line is a horizontal line and a vertical asymptote means the imaginary line is a vertical line.a.) What is the vertical asymptote for y=log2(x)(rightmost function in black)? b.) What is the vertical asymptote for the transformed function (leftmost function in green)? c.) Complete the table of values for y=log2(x). x y 0 1 2d.) Complete the table of values from the green function graphed above.x y -1 0 2e) Comparing the asymptotes and table of values, describe the two transformations that were carried out on y=log2(x)

Answer 1

a) We have to find the vertical asymptote of the function:

`y=\log _2(x)`

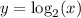
Logarthimic functions have positive values for arguments that are greater than 1 and negative for values between 0 and 1.

The values of y tend to minus infinity when approaching x = 0. Then, x = 0 is the vertical asymptote of y.

b) We can see in the graph that the green function is translated 2 units to the left (NOTE: this is not the only transformation, but is the one that affects the vertical asymptote location).

Then, the vertical asymptote is located at x = -2.

c) We can complete the table as:

x y

0 -∞

1 0

2 1

d) We can complete the table as:

x y

-1 3

0 4

2 5

e) We have to identify all the transformations that transform y = log2(x) to the green line.

We have already see that, because of the position of the asymptotes, there is a translation two units to the left.

As the x-intercept is not 2 units to the left, we can infere that there is a translation up or a scale.

If we look at the black line and we translate two units to the left, the green line should intercept the x-axis at x = 1-2 = -1. As the value of the green line is y = 3 instead of 0, we can conclude that we also have a translation 3 units up.

Then, we have a translation 2 units to the left and 3 units up.

We can write the equation as:

`y_g=\log _2(x+2)+3`