48√3 u² (or 83.14 u²)
1) Since the question mentions a radius and a regular triangle, then we can sketch out an inscribed triangle:
2) So, we can write out the following about it, every angle is 60º. Also, we have two right triangles below.
The triangle below is a special right triangle 30º 60º 90º. And prolonging a line segment we can trace 6 right triangles:
3) Now let's find the height of that triangle:
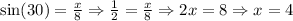
To find out the base, another trig ratio:
![\begin{gathered} \cos (30)=(y)/(8) \\ \frac{\sqrt[]{3}}{2}=(y)/(8) \\ 2y=8\sqrt[]{3} \\ y=4\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9owl1b2n6p81p6yckvmt11r2yawkq01d91.png)
3) Finally let's plug into the Area of a Triangle, and then multiply it by 6. To find the area of that larger triangle:
![A=6((1)/(2)\cdot4\sqrt[]{3}\cdot4)\Rightarrow A=48\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/7k7mvfxdvkx8hpm7kitezaep5ntj2ehkt5.png)
Hence, the answer is 48√3