A sailboat cost 31,567. You pay 20% down and amortize the rest with the equal monthly payments over 14- year period. If you must pay 6.6 compounded monthly , what is your monthl…

Question

asked Jul 27, 2023 173k views

1 Answer

Wilduck · Answer 1 · 2023-08-01T20:13:21+0000

The annuity formula is given to be:

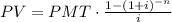
$PV=PMT\cdot(1-(1+i)^(-n))/(i)$

where

PV = Present Value

PMT = Periodic Payment

i = Interest Rate

n = Number of Periods

If one is to pay 20% down, the loan percentage will be:

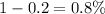
$1-0.2=0.8\%$

Therefore, the loan amount will be:

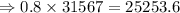
$\Rightarrow0.8*31567=25253.6$

The interest rate is 6.6%. The monthly rate will therefore be:

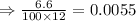
$\Rightarrow(6.6)/(100*12)=0.0055$

The number of periods over 14 years is gotten to be:

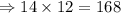
$\Rightarrow14*12=168$

Therefore, we have the following parameters to work with:

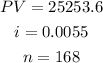
$\begin{gathered} PV=25253.6 \\ i=0.0055 \\ n=168 \end{gathered}$

To calculate the PMT, we can rewrite the annuity formula to give:

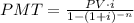
$PMT=(PV\cdot i)/(1-(1+i)^(-n))$

Therefore, we can solve to be:

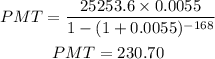
$\begin{gathered} PMT=(25253.6*0.0055)/(1-(1+0.0055)^(-168)) \\ PMT=230.70 \end{gathered}$

Therefore, the monthly payment is 230.70.

The amount paid is given to be:

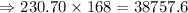
$\Rightarrow230.70*168=38757.6$

Therefore, the interest paid is:

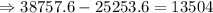
$\Rightarrow38757.6-25253.6=13504$

Therefore, the interest paid is 13,504.