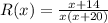
(a)
Since we can't divide by 0, we need to check the denominator in order to find the restrictions over the domain:
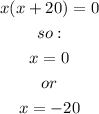
Therefore, the domain is:
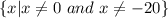
Answer:
B
------------------------------
(b)
The vertical asymptotes are located at the restriction points. So, the vertical asymptotes are:
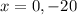
----------------------
(c)
Since:
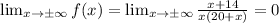
We can conclude that the horizontal asymptote is located at:
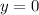
(d)
Answer:
A