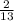Question

You randomly select one card from a 52-card deck. Find the probability of selecting a six or a nine.

Answer 1

Given:

• Number if cards in a deck = 52

Let's find the probability of selecting a six or a nine if you randomly select one card from the 52-card deck.

To find the probability, apply the formula:

`P(\text{six or nine)= P(six) + P(nine)}`

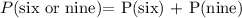
Where:

• Number of six's in a deck = 4

,

• Number of nine's in a deck = 4

Thus, we have:

`\begin{gathered} P(six)=(4)/(52) \\ \\ P(nine)=(4)/(52) \\ \\ P(\text{six or nine)=}(4)/(52)+(4)/(52) \\ \\ P(\text{six or nine) = }(4+4)/(52)=(8)/(52)=(2)/(13) \end{gathered}`

Therefore, the pprobability of selecting a six or a nine is 2/13.

ANSWER:

`(2)/(13)`