1 Answer

Lukas Barth · Answer 1 · 2023-06-24T10:00:04+0000

We are given the following functions:

$\begin{gathered} f\mleft(x\mright)=2x+1,\text{ and} \\ g\mleft(x\mright)=3x^2-1 \end{gathered}$

We are asked to determine the following:

$(f\circ g)(x)$

This is a composition of functions and it is equivalent to the following:

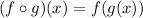
$(f\circ g)(x)=f(g(x))$

This means that we will substitute the value of "x" is f(x) for the function g(x), like this:

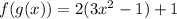
Now we simplify, first by applying the distributive property:

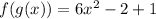
Now we solve the operation:

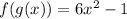
And thus we have the composition of the functions.

For part B we are asked:

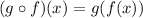
$(g\circ f)(x)=g(f(x))$

This means that this time we will substitute the value of "x" in g(x) for the function f(x), like this:

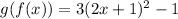
Now we simplify the function. First, we solve the square using the following relationship:

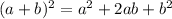
Using the relationship we get:

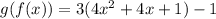
Now we apply the distributive property:

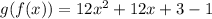
Now we solve the operations:

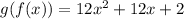
And thus we get the composition of the functions.

Please log in or register to add a comment.